Lester Caudill, University of Richmond
Editor’s note: The question everyone in the world wants answered is how far the new coronavirus will spread and when the pandemic will begin to ebb. To know that, epidemiologists, public health authorities and policymakers rely on models.
Models are not meant to predict the future perfectly – yet they’re still useful. Biomedical mathematician Lester Caudill, who is currently teaching a class focused on COVID-19 and modeling, explains the limitations of models and how to better understand them.
What are infectious disease models?
Mathematical models of how infections spread are simplified versions of reality. They are designed to mimic the main features of real-world disease spread well enough to make predictions which can, at least partly, be trusted enough to make decisions. The COVID-19 model predictions reported in the media come from mathematical models that have been converted into computer simulations. For example, a model might use a variety of real world data to predict a date (or range of dates) for a city’s peak number of cases.
Why is modeling the spread of COVID-19 challenging?
In order for a model’s predictions to be trustworthy, the model must accurately reflect how the infection progresses in real life. To do this, modelers typically use data from prior outbreaks of the same infection, both to create their model, and to make sure its predictions match what people already know to be true.
This works well for infections like influenza, because scientists have decades of data that help them understand how flu outbreaks progress through different types of communities. Influenza models are used each year to make decisions regarding vaccine formulations and other flu-season preparations.
By contrast, modeling the current COVID-19 outbreak is much more challenging, simply because researchers know very little about the disease. What are all the different ways it can be transferred between people? How long does it live on door knobs or Amazon boxes? How much time passes from the moment the virus enters a person’s body until that person is able to transmit it to someone else? These, and many other questions, are important to incorporate into a reliable model of COVID-19 infections. Yet people simply do not know the answers yet, because the world is in the midst of the first appearance of this disease, ever.
Why do different models have different predictions?
The best modelers can do is assume some things about COVID-19, and create models that are based on these assumptions. Some current COVID-19 models assume that the virus behaves like influenza, so they use influenza data in their models. Other COVID-19 models assume that the virus behaves like SARS-CoV, the virus that caused the SARS epidemic in 2003.
Other models may make other assumptions about COVID-19, but they must all assume something, in order to make up for information that they need, but that simply does not yet exist. These different assumptions are likely to lead to very different COVID-19 model predictions.
How can people make sense of the different – sometimes conflicting – model predictions?
This question gets at, perhaps, the most important thing to know about mathematical model predictions: They are only useful if you understand the assumptions that the model is based on.
Ideally, model predictions like, “We expect 80,000 COVID-related deaths in the U.S.” would read more like, “Assuming that COVID-19 behaves similar to SARS, we expect 80,000 COVID-related deaths in the U.S.” This helps place the model’s prediction into context, and helps remind everyone that model predictions are not, necessarily, glimpses into an inevitable future.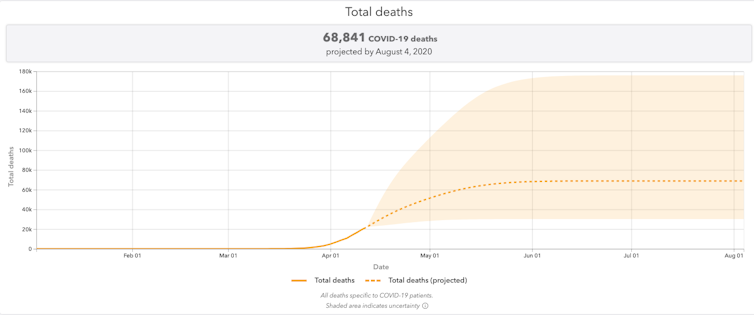
It may also be useful to use predictions from different models to establish reasonable ranges, rather than exact numbers. For instance, a model that assumes COVID-19 behaves like influenza might predict 50,000 deaths in the U.S. Rather than trying to decide which prediction to believe – which is an impossible task – it may be more useful to conclude that there will be between 50,000 and 80,000 deaths in the U.S.
Why do the same models seem to predict different outcomes today than they did yesterday?
As COVID-19 data becomes available – and there are many good people working tirelessly to gather data and make it available – modelers are incorporating it so that, each day, their models are based a little more on actual COVID-19 information, and a little less on assumptions about the disease. You can see this process unfold in the news, where the major predictive COVID-19 models provide almost daily revisions to their prior estimates of case numbers and deaths.
Can a model that’s (probably) not accurate at predicting the future still be useful?
While models of infections can provide insights into what the future might hold, they are far more valuable when they help answer, “How can policies alter that future?”
For instance, a baseline model for predicting the future number of COVID-19 cases might be adapted to incorporate the effects of, say, a stay-at-home order. By running model simulations with the order, and comparing to model simulations without the order, public health authorities may learn something about how effective the order is expected to be. That can be especially useful when comparing the associated costs, not only in terms of disease burden, but in economic terms, as well.
One step further, this same model could be used to predict the consequences of ending the order on, say, June 10 – the current target date for the stay-at-home order in Virginia – and compare them to model predictions for ending the order on, say, May 31 or June 30. Here, as in many other settings, models prove to be most useful when they’re used to generate different scenarios which are compared to each other. This is different than comparing model predictions to reality.
[Get our best science, health and technology stories. Sign up for The Conversation’s science newsletter.]
Lester Caudill, Professor of Mathematics, University of Richmond
This article is republished from The Conversation under a Creative Commons license. Read the original article.

